Category Archives: FAQ

CODE, Computing and fitting spectra, FAQ, Optical constants, Optical modeling, SCOUT, Uncategorized

How to develop flexible optical constant models based on given n and k tables

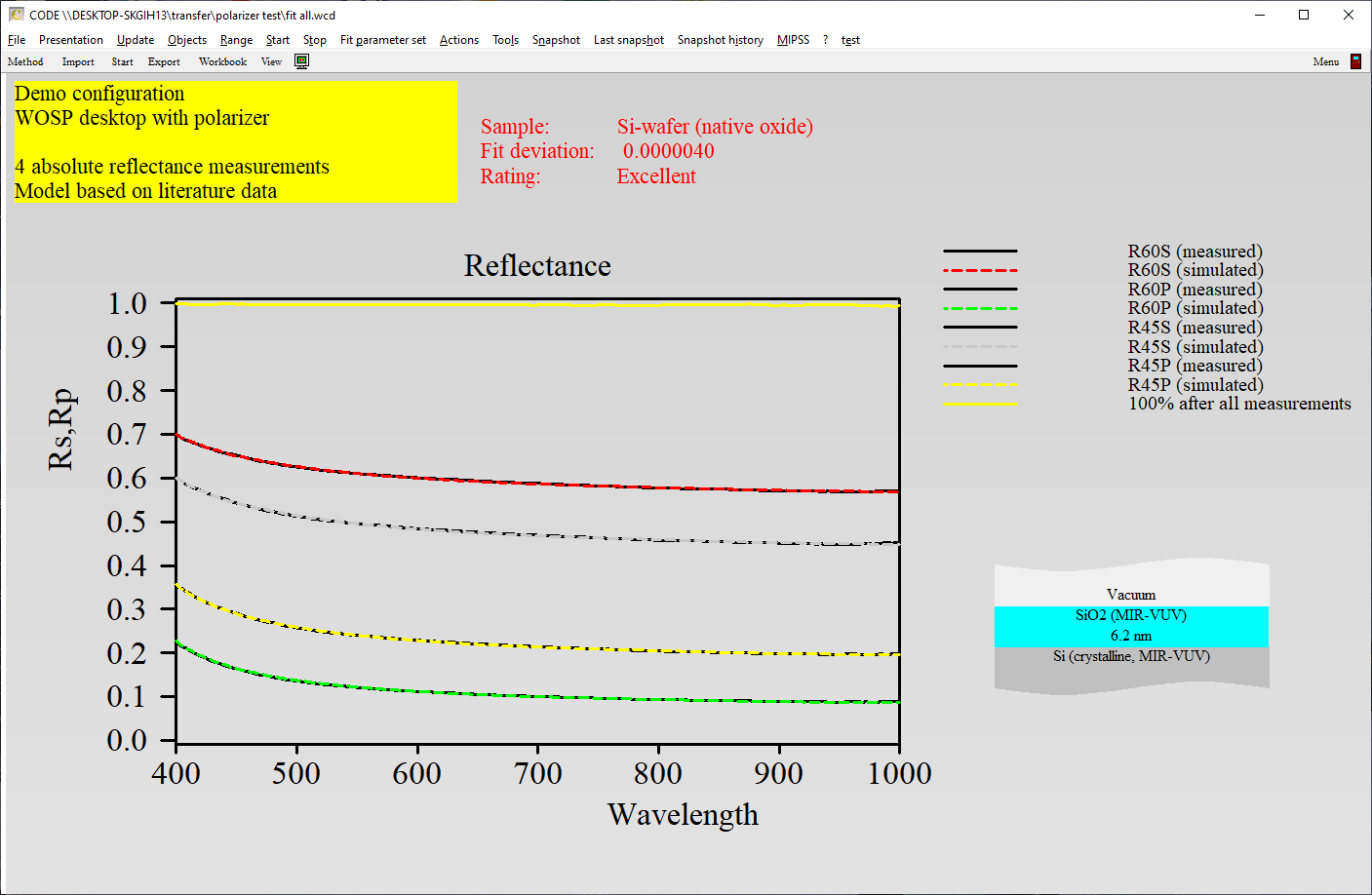
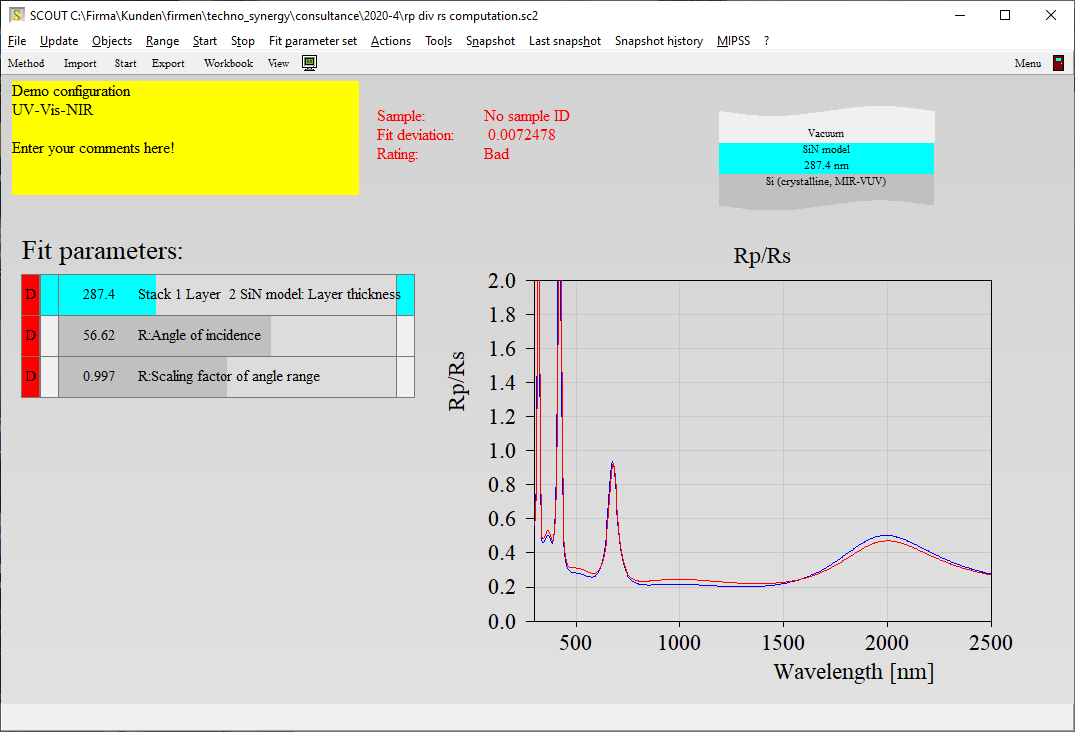
Materials used in thin films may differ in their optical constants n and k from the corresponding bulk versions. Even if you find optical constant tables in literature for your application you may need to make some adjustments to the n and k values. This is certainly difficult if you have just a table of fixed values – what you need is a flexible model which can adjust the spectral shape of n and k by modifying a few key parameters only. This short tutorial shows how to proceed in such a case.

Crystalline silicon is used as example. The database of our SCOUT and CODE software packages contain several silicon versions. Here I have selected the item ‘Silicon (crystalline, MIR-VUV)’. These are the n and k data, featuring several interband transitions and a slow decay of k towards the indirect band gap around 1.1 eV: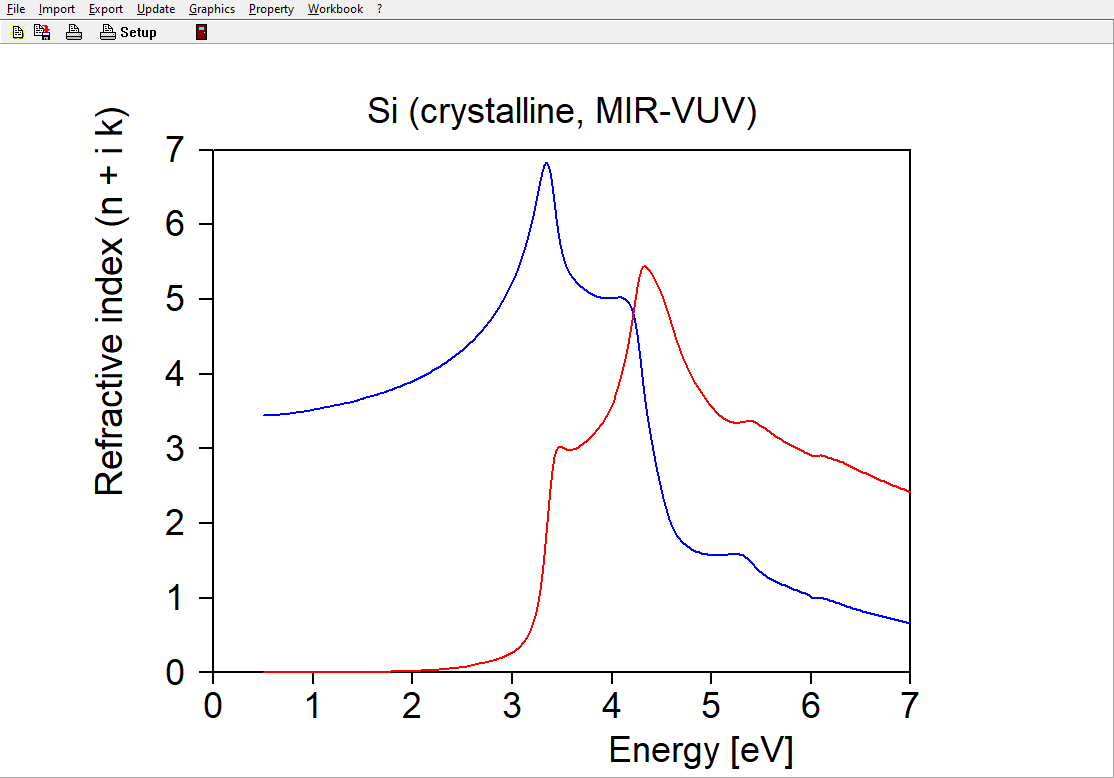

If you change the temperature of a silicon wafer or deposit poly-crystalline silicon thin films you may observe similar structures but not exactly the same n and k – a flexible model would be nice to have. Our strategy to develop such a model will be this: First, we generate ‘measured data’ which are computed using the existing n and k table values. Then, in the second step, we setup a suitable model and adjust its parameters to reproduce the ‘measured’ data. If the ‘measurements’ provide enough information the n and k values of the model should be almost the same as those of the original table.

Since we will simulate the measurements we can easily work with a system which would be almost impossible to realize. In order to clearly ‘see’ the weak silicon absorption in the visible we use a 2 micron thick free standing layer – this layer is quite transparent and it will generate a nice interference pattern. To match the amplitude of the fringes will be difficult with wrong k values – so this setup ensures good n and k data of the model in the visible and NIR. The layer stack is this:

Using this layer stack we could now generate several reflectance and transmittance spectra, taken at various angles of incidence. This would make a nice set of ‘measured data’ for the fit procedure. However, to make our life as easy as possible we can use an ellipsometry object in the list of spectra. Objects of this type have the option to compute so-called ‘Pseudo n and k’ values. With this option the ellipsometric angles Psi and Delta are represented by pseudo n and k values of a virtual single interface. In spectral regions where our silicon layer is opaque the pseudo n and k values are the same as the real ones. In the transparent region the pseudo n and k values reflect the interference structures – this looks strange, and one could certainly question the usefulness of the concept ‘Pseudo n and k’. However, the interference pattern is what we go for to get good small k values in the model. The blue curves below show the generated pseudo n and k values. Within this example we will work in the spectral range 200 … 1000 nm: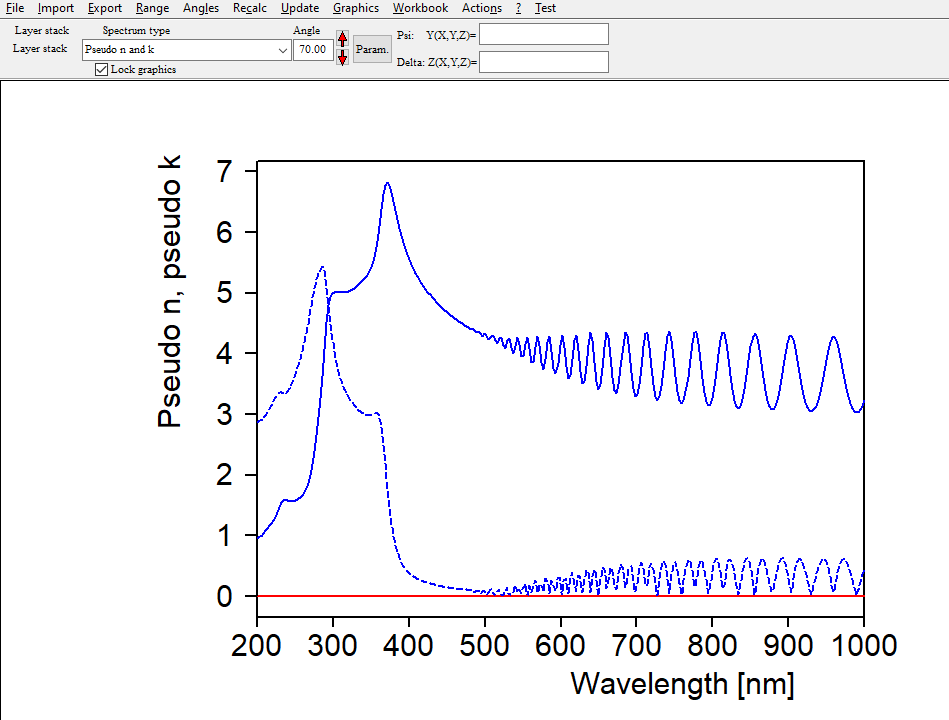

Ellipsometry objects offer the local menu command ‘Actions / Use simulated data as measured data’ which is what we need now. The blue curves are now copied to the red measurement data as if we had imported measured data.

We can now replace the material object by our first model in the layer stack. I have started with a very simple model which consists of a constant real part of the refractive index and a Tauc-Lorentz model (inside a KKR susceptibility object). It is a good idea to generate a new item of type ‘Multiple spectra view’ which can show both the original table values of n and k and the model values in one graph (lower left side). With this simple model, you cannot expect a good match since  silicon shows several interband transitions in the range 200 … 1000 nm: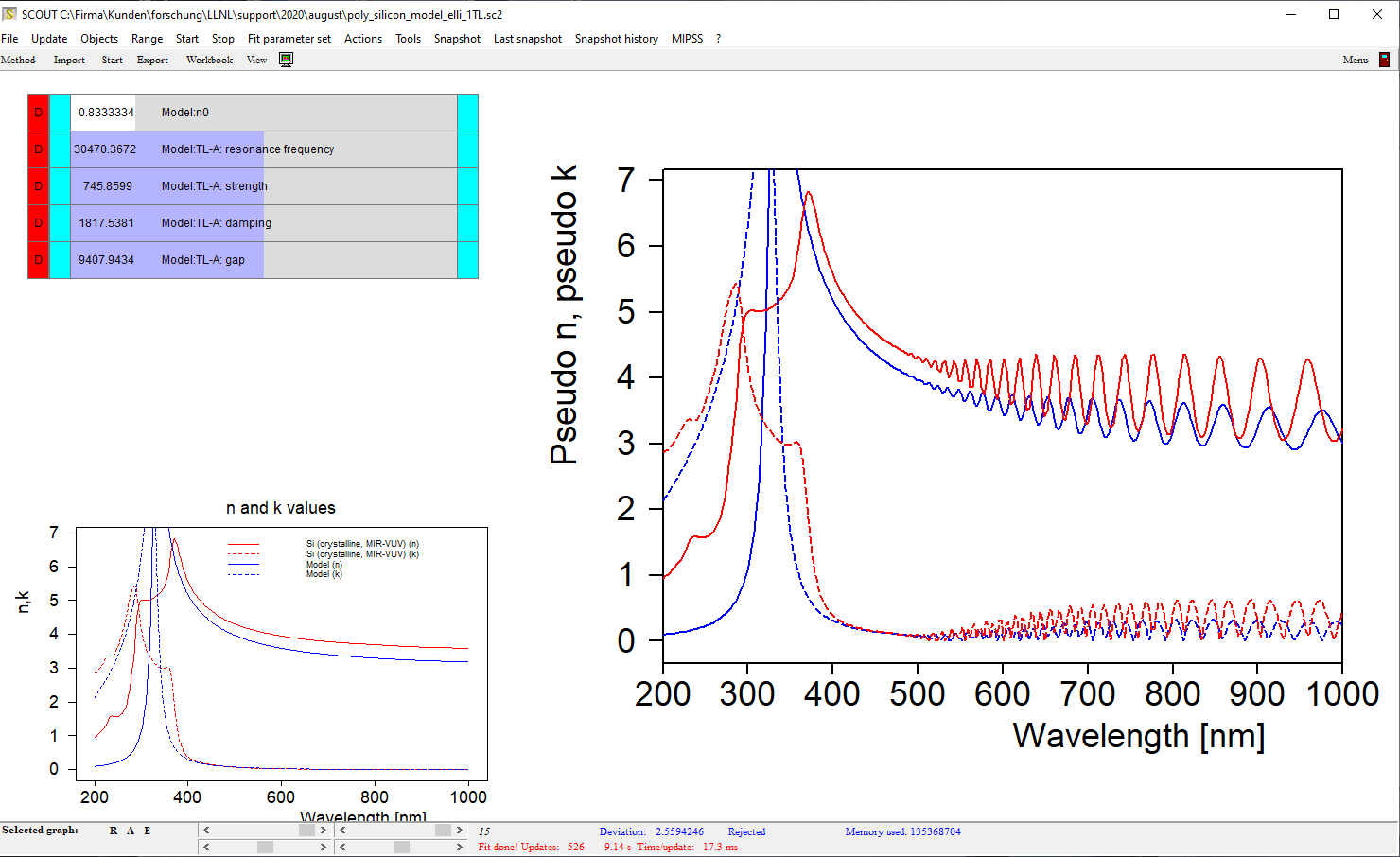

However, if we limit the range to 400 … 1000 nm the simple model works quite well:

For the full range (200 … 1000 nm) we need more interband transitions. Sticking to the Tauc-Lorentz oscillator type, I have added 2 more which brings up to a new level (still not satisfying, though):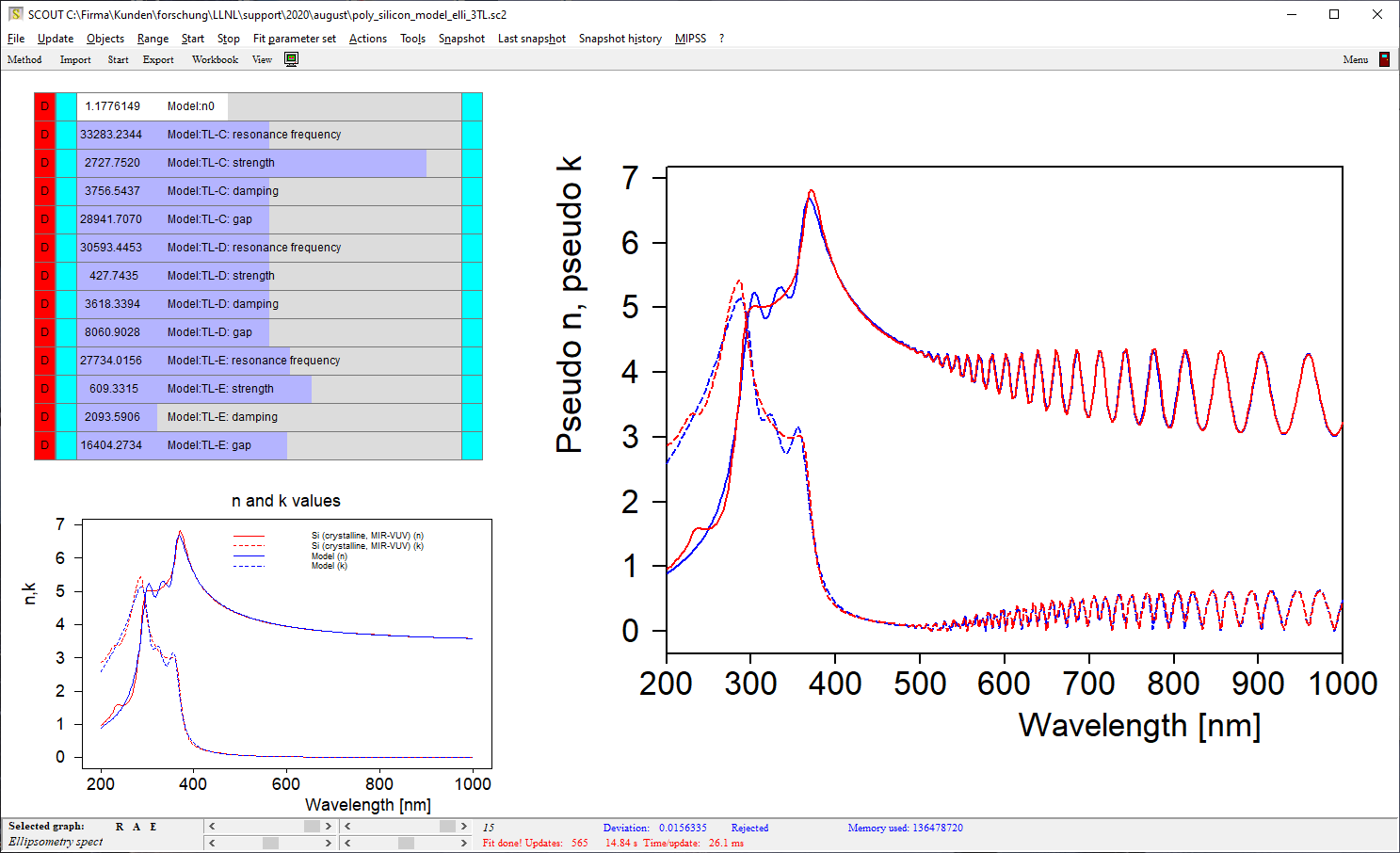

Depending on your patience (and the needs of the final application) you can add more features as you like, approaching the former table values of n and k more and more. I stopped my example at this level: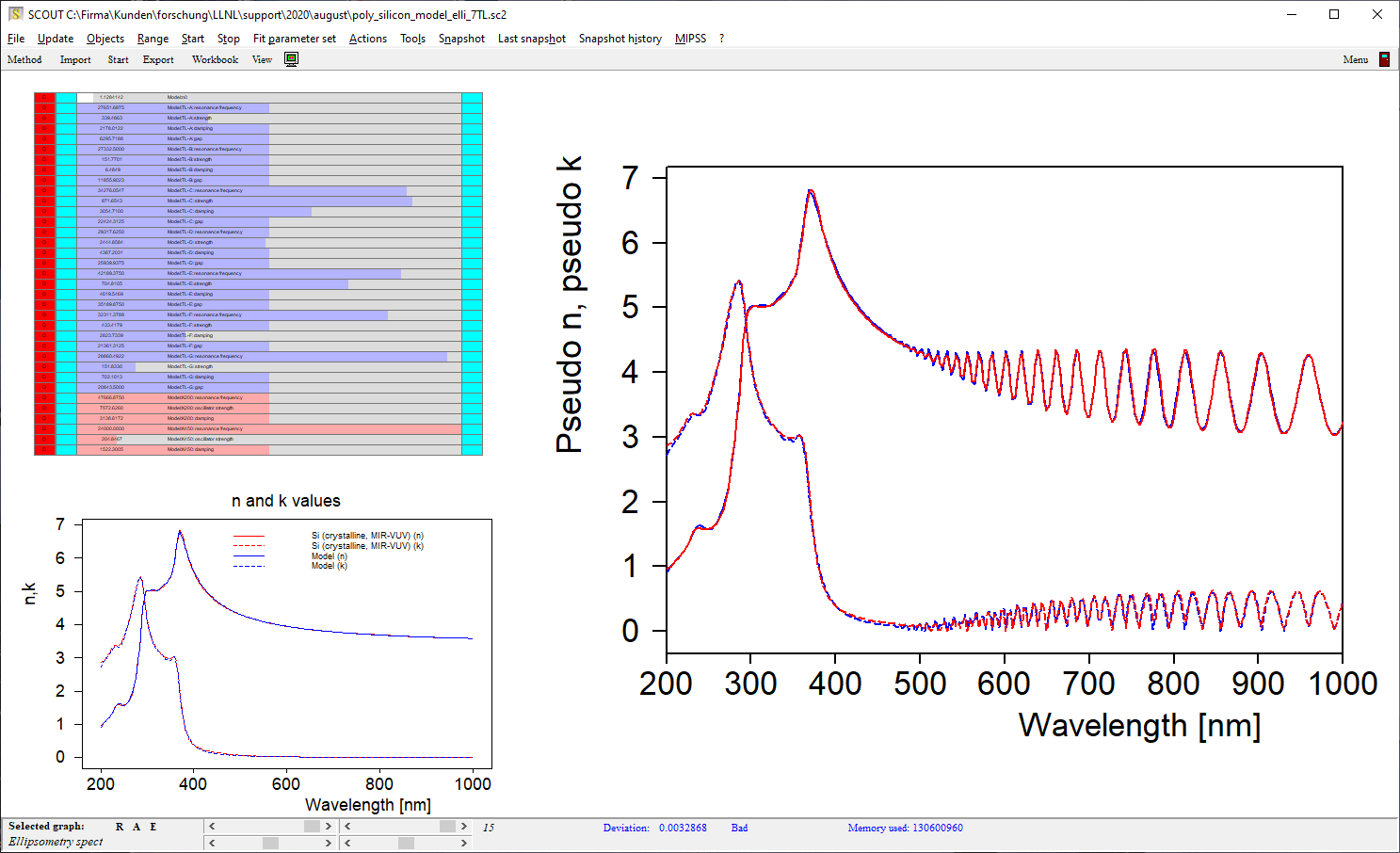

The model developed for silicon this way can now be saved to the optical constant database for future use. You can use it for studies of systematic variations of deposition conditions and generate tables like ‘resonance frequency vs deposition temperature’.

You can follow the strategy shown in this tutorial for all kinds of materials, as long as you get good tabulated values of n and k to start with.

CODE, OLE automation, SCOUT, Uncategorized

New OLE commands exporting spectra

The new OLE command export_spectra_via_variants has been introduced in both SCOUT and CODE (object generation 5.14). The command takes 5 parameters:

  • input: the index of the spectrum object in the list of spectra (counting 1, 2, 3, …)
  • output: a variant array holding the spectral positions (e.g. wavelengths)
  • output: a variant array with simulated spectral values
  • output: a variant array with measured spectral values at the same spectral positions as the simulated values, obtained by linear interpolation between the closest available points
  • output: a string with the spectral unit

 

BREIN, CODE, Computing and fitting spectra, SCOUT, Uncategorized

Fit parameter sets embedded in configuration file

Starting with object generation 5.12, you can store fit parameter sets in a list called ‘Fit parameter pool’.  This list is stored as part of the SCOUT or CODE configuration file. Using fit parameter sets from the pool avoids the necessity to load them from separate files.

Instead of specifying a filename for the fit parameter set (which is still possible) you can use phrases like ‘pool(step 1)’ or ‘pool(oscillator strengths only)’ to load fit parameter sets with names ‘step 1’ or ‘oscillator strengths only’.

Using file based fit parameter sets is possible after all, of course.

CODE, Company, Hardware, Optical modeling, SCOUT, Uncategorized

Polarizer for R and T measurements

We have added a polarizer to our desktop R and T measurement system. The same polarizer can be used for all systems recording R and T for shiny, non-scattering samples.

The desktop system records the 100% signal when detector and light source are positioned directly opposite to each other:

After this measurement you can do absolute reflectance measurements at arbitrary angles of incidence. We have generated tools to conveniently set fixed angles of incidence – here we have used 45° and 60°.

The graph below shows 4 absolute spectra of a silicon wafer (45°, 60°, s- and p-polarization). We could achieve almost perfect match of simulated spectra based on literature data of the optical constants, fitting a thickness of 6.2 nm of the native SiO2 layer on the wafer. Data acquisition for each spectrum took less than 1 second (averaging 18 spectra using an integration time of 50 ms).

BREIN, CODE, Computing and fitting spectra, Optical modeling, SCOUT, Uncategorized

Angle of incidence distribution

Spectroscopic experiments can never realize single angle of incidence but have to work with a (continuous) distribution of angles. Although in most cases the assumption of a single angle of incidence is a very good approximation there are cases where we need to take into account more details in producing simulated spectra. One example is taking reflectance spectra of small spots with a microscope objective, using a large cone of incident radiation.

For a long time our software packages can compute spectra averaged for a set of incidence angles, each one defined by the value of the angle and a weight. We have now implemented new features to simplify work in this field.

If you have prepared a list of angles of incidence you can now connect these angles to the angle of incidence that you have defined for spectrum object which owns the list of angles. You can check the option as shown here:

If you have activated this option you can use a set of angles with positive and negative values (centered around 0) as shown here:

If the angle of the parent object is 50° the computation of the spectrum is done for the 3 angles 45°, 50° and 55°, with weights 0.3, 0.4 and 0.3, respectively. If you have declared the angle of the parent object to be a fit parameter the set of 3 angles is moved automatically when the value of the center angle changes during the fit. This helps to adjust the distribution of angles to match the experimental settings.

Finally, there is a new fit parameter called ‘Scaling factor of angle range’. This number scales the distance of the individual angles to the center angle: If the factor is 1.0 the original angles are used. If the factor is 0.1, for example, a value of 5° becomes 0.5°. Varying the factor between 0.1 and 2 in the example shown above, you can compute spectra for a distributions between -0.5° … 0.5° to -10° … 10°.

We hope that this new flexibility helps to achieve better fitting results for spectra measured with microscopes or other systems with spectra features depending critically on the angle of incidence.

BREIN, CODE, Optical modeling, SCOUT, Uncategorized

New spectrum type

Starting with object generation 5.11 we have introduced a new spectrum type called ‘Rp/Rs’. If you select this option the spectrum object computes the ratio of the intensity reflectance for p-polarized light and s-polarized light. This ratio can be directly fitted to experimental data if your measurement system produces this quantity as final result.

CODE, Data import, SCOUT, Uncategorized

Optoplex NGQ import more flexible

Zeiss Optoplex NGQ files may have a row with explicit wavelength values – or not.

If wavelength information is present there is an empty line before and after the row with wavelength values. We rely on the assumption that the generated wavelength values are equidistant.

In the case of missing wavelength information we count the number of spectral points. It is assumed that the first one belongs to a wavelength of 380 nm, and that the difference between neighbored points is always 5 nm.

Our software can now import NGQ files  both with and without wavelength row.

BREIN, CODE, Data import, SCOUT, Uncategorized

Bugfix for corrupted configuration files

Having investigated a case where CODE stopped working after importing an older method, we found that a data field contained numbers marked as NAN (= not a number). Up to now we don’t know how this situation can arise – probably it was caused by a failing import of measured data.

The following mechanisms have been implemented to make the software survive this situation (active starting with object generation 5.09):

  • Directly after loading numbers marked as NAN are replaced by zeroes. This check is done for configurations stored with generations lower than 5.09.
  • Starting with object generation 5.09, numbers of data fields are checked for NAN status (and replaced by zeroes if necessary) before they are saved in a configuration file.
  • After each import of measured data the relevant data field is checked for NAN status and eventually corrected.